|
|
|
$$2p = B + b + L + h$$
Perimetro
$$A = \frac{\left(B + b \right) \times h}{2}$$
Area
$$B + b = \frac{2A}{h}$$
Somma basi
$$h = \frac{2A}{B + b}$$
Altezza
$$p_{1} = B - b$$
Proiezione lato obliquo
$$B - b = p_{1}$$
Differenza basi
$$B = b + p_{1}$$
$$b = B - p_{1}$$
Tr. Rettangolo formato da altezza - lato obliquo
$$L = \sqrt{ {p_{1}}^2 + {h}^2 }$$
Lato (Teorema di Pitagora)
$$p_{1} = \sqrt{ {L}^2 - {h}^2 }$$
Proiezione lato obliquo
$$h = \sqrt{ {L}^2 - {p_{1}}^2 }$$
Altezza
Tr. Rettangolo formato da altezza - diagonale maggiore
$$d_{1} = \sqrt{ {B}^2 + {h}^2 }$$
Diagonale maggiore (Teorema di Pitagora)
$$B = \sqrt{ {d_{1}}^2 - {h}^2 }$$
Base maggiore
$$h = \sqrt{ {d_{1}}^2 - {B}^2 }$$
Altezza
Tr. Rettangolo formato da altezza - diagonale minore
$$d_{2} = \sqrt{ {b}^2 + {h}^2 }$$
Diagonale minore (Teorema di Pitagora)
$$b = \sqrt{ {d_{2}}^2 - {h}^2 }$$
Base minore
$$h = \sqrt{ {d_{2}}^2 - {b}^2 }$$
Altezza
Definizione
Un trapezio rettangolo è un trapezio con un angolo retto (90 gradi).
Proprietà
- Ha un un angolo retto (90 gradi)
- Sono valide tutte le formule del Trapezio qualsiasi
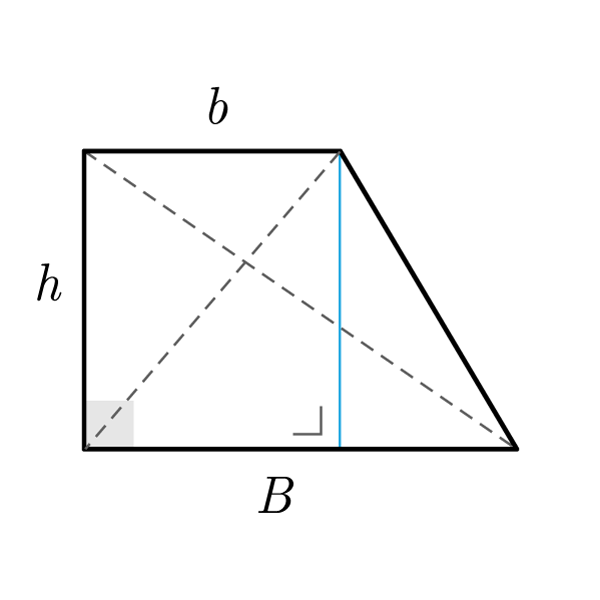
Formule Trapezio rettangolo
| Dato | Formula |
|---|---|
| Perimetro | 2p = B + b + L + h |
| Area | A = [(B + b) × h] / 2 |
| Altezza | h = (2 × A) / (B + b) |
| Proiezione lato obliquo | p1 = B - b |
| Somma basi | B + b = (2 × A) / h |
| Somma basi | B + b = 2p - 2 × L |