|
|
|
$$2p = L \times 4$$
Perimetro
$$L = \frac{2p}{4}$$
$$A = {L}^{2}$$
Area
$$L = \sqrt{A}$$
$$d = L \sqrt{2}$$
Diagonale
$$L = \frac{d}{\sqrt{2}}$$
$$A = \frac{{d}^{2}}{2}$$
Area
$$d = \sqrt{2A}$$
Definizione
Un quadrato è un poligono con quattro lati e quattro angoli congruenti (tutti retti).
Proprietà
- Quattro lati congruenti
- Quattro angoli retti congruenti
- Le diagonali sono perpendicolari
- La diagonale forma due triangoli rettangoli congruenti. In particolare ogni triangolo ha angoli di 45°, 45°, 90°
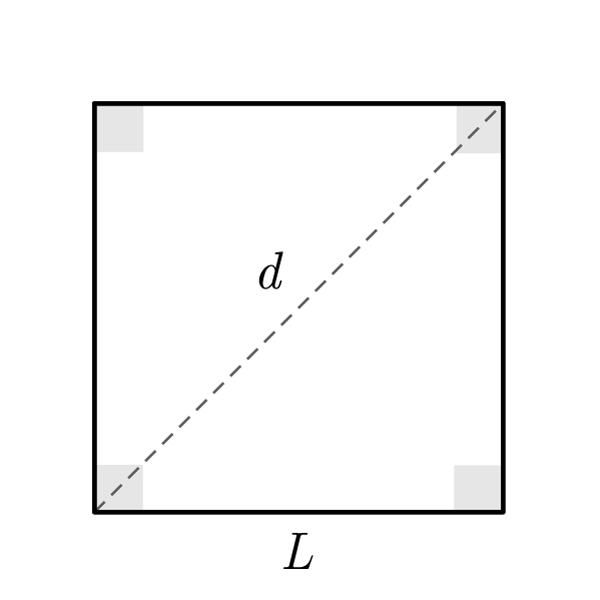
Formule Quadrato
| Dato | Formula |
|---|---|
| Perimetro | 2p = L × 4 |
| Area | A = L2 |
| Lato | L = 2p / 4 |
| Lato | L = √A |
| Diagonale | d = L × √2 |
| Lato | L = d / √2 |
| Area | A = d2 / 2 |
| Diagonale | d = √(2A) |