|
|
|
$$V = \frac{A_{base} \times h}{3}$$
Volume
$$A_{base} = \frac{3V}{h}$$
Area base
$$h = \frac{3V}{A_{base}}$$
Altezza
$$S_{tot} = A_{base} + S_{lat}$$
Superficie totale
$$S_{lat} = S_{tot} - A_{base}$$
Superficie laterale
$$A_{base} = S_{tot} - S_{lat}$$
Area base
Piramide retta
$$S_{lat} = \frac{2p \times a}{2}$$
Superficie laterale
$$2p = \frac{2 \times S_{lat}}{a}$$
Perimetro base
$$a = \frac{2 \times S_{lat}}{2p}$$
Apotema
$$r = \frac{2 \times A_{base}}{2p}$$
Raggio inscritto
$$2p = \frac{2 \times A_{base}}{r}$$
Perimetro base
$$A_{base} = \frac{2p \times r}{2}$$
Area base
Usando il Teorema di Pitagora
$$a = \sqrt{{h}^2 + {r}^2}$$
Apotema
$$r = \sqrt{{a}^2 - {h}^2}$$
Raggio di base
$$h = \sqrt{{a}^2 - {r}^2}$$
Altezza
Piramide quadrangolare
$$A_{base} = {L}^2$$
Area base
$$L = \sqrt{A_{base}}$$
Spigolo di base
$$2p = L \times 4$$
Perimetro base
$$L = \frac{2p}{4}$$
Spigolo di base
$$r = \frac{L}{2}$$
Raggio di base
$$L = 2 r$$
Spigolo di base
Definizione
Una piramide è un poliedro costituito da una faccia poligonale, detta base, e da un punto esterno alla base, detto vertice.
Proprietà
- In una piramide sono presenti una faccia di base e le facce laterali
- Le facce laterali di una piramide sono triangoli isosceli congruenti tra loro
- Altezza: segmento perpendicolare che congiunge il vertice della piramide con il piano che contiene la base
- Apotema: nella piramide regolare, segmento che congiunge il vertice con il punto medio dello spigolo di base. Coincide con l'altezza di uno dei triangoli che compongono le facce laterali
Altre definizioni
- Una piramide retta è una piramide in cui il poligono di base è inscrivibile in una circonferenza, e l'altezza congiunge il vertice con il centro della circonferenza inscritta.
- Una piramide obliqua è una qualsiasi piramide che non sia retta
- Una piramide regolare è una piramide avente per base un poligono regolare
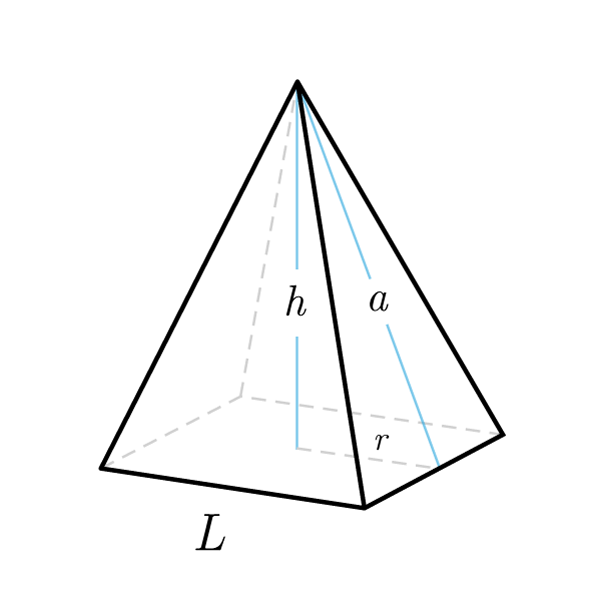
Formule Piramide
| Dato | Formula |
|---|---|
| Volume | V = (Abase × h) / 3 |
| Area base | Abase = (3V) / h |
| Altezza | h = (3V) / Abase |
| Superficie totale | Stot = Abase + Slat |
| Superficie laterale | Slat = Stot - Abase |
| Area base | Abase = Stot - Stot |
Formule Piramide retta
| Dato | Formula |
|---|---|
| Superficie laterale | Stot = (2p × a) / 2 |
| Perimetro base | 2p = (2 × Slat) / a |
| Apotema | a = (2 × Slat) / 2p |
| Raggio inscritto | r = (2 × Abase) / 2p |
| Perimetro base | 2p = (2 × Abase) / r |
| Area base | Abase = (2p × r) / 2 |
| Apotema | a = √(h2 + r2) |
| Raggio di base | r = √(a2 - h2) |
| Altezza | h = √(a2 - r2) |
Formule Piramide quadrangolare
| Dato | Formula |
|---|---|
| Superficie laterale | Abase = L2 |
| Spigolo di base | L = √(Abase) |
| Perimetro base | 2p = L × 4 |
| Spigolo di base | L = (2p) / 2 |
| Raggio di base | r = L/2 |
| Spigolo di base | L = 2r |